Dijkstra’s Algorithm for Adjacency List Representation | Greedy Algo-8

We recommend reading the following two posts as a prerequisite for this post.

1. Greedy Algorithms | Set 7 (Dijkstra’s shortest path algorithm)
2. Graph and its representations

We have discussed Dijkstra’s algorithm and its implementation for adjacency matrix representation of graphs. The time complexity for the matrix representation is O(V^2). In this post, O(ELogV) algorithm for adjacency list representation is discussed.
As discussed in the previous post, in Dijkstra’s algorithm, two sets are maintained, one set contains a list of vertices already included in SPT (Shortest Path Tree), and another set contains vertices not yet included. With adjacency list representation, all vertices of a graph can be traversed in O(V+E) time using BFS. The idea is to traverse all vertices of the graph using BFS and use a Min Heap to store the vertices not yet included in SPT (or the vertices for which the shortest distance is not finalized yet). Min Heap is used as a priority queue to get the minimum distance vertex from a set of not yet included vertices. The time complexity of operations like extract-min and decrease-key value is O(LogV) for Min Heap.

Following are the detailed steps.

1. Create a Min Heap of size V where V is the number of vertices in the given graph. Every node of the min-heap contains the vertex number and distance value of the vertex.
2. Initialize Min Heap with source vertex as root (the distance value assigned to source vertex is 0). The distance value assigned to all other vertices is INF (infinite).
3. While Min Heap is not empty, do the following :
   1. Extract the vertex with minimum distance value node from Min Heap. Let the extracted vertex be u.
   2. For every adjacent vertex v of u, check if v is in Min Heap. If v is in Min Heap and the distance value is more than the weight of u-v plus the distance value of u, then update the distance value of v.

   Let us understand with the following example. Let the given source vertex be 0
   

   

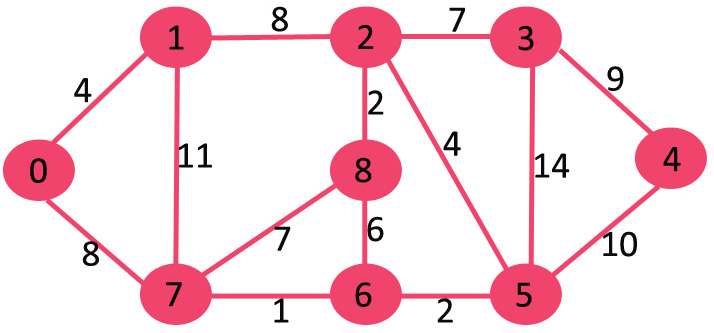
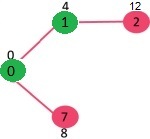
   Initially, the distance value of the source vertex is 0 and INF (infinite) for all other vertices. So source vertex is extracted from Min Heap and distance values of vertices adjacent to 0 (1 and 7) are updated. Min Heap contains all vertices except vertex 0.
   The vertices in green color are the vertices for which minimum distances are finalized and are not in Min Heap
   

   

   Since the distance value of vertex 1 is minimum among all nodes in Min Heap, it is extracted from Min Heap and distance values of vertices adjacent to 1 are updated (distance is updated if the vertex is in Min Heap and distance through 1 is shorter than the previous distance). Min Heap contains all vertices except vertex 0 and 1.
   

   

   Pick the vertex with a minimum distance value from the min-heap. Vertex 7 is picked. So min-heap now contains all vertices except 0, 1, and 7. Update the distance values of adjacent vertices of 7. The distance value of vertex 6 and 8 becomes finite (15 and 9 respectively).
   

   

   Pick the vertex with a minimum distance from the min-heap. Vertex 6 is picked. So min-heap now contains all vertices except 0, 1, 7, and 6. Update the distance values of adjacent vertices of 6. The distance value of vertex 5 and 8 are updated.
   

   

   The above steps are repeated till the min-heap doesn’t become empty. Finally, we get the following shortest-path tree.
   

   

   Below is the implementation of the above approach: